데이터로 물리 법칙을 찾다: PDE-FIND로 알아보는 데이터 기반 편미분방정식 발견

과학과 공학의 많은 문제들은 **편미분방정식(PDE, Partial Differential Equation)**으로 표현됩니다. 유체의 흐름, 확산 현상, 파동 전파 등 우리가 접하는 수많은 자연현상이 PDE에 의해 기술되지요. 하지만 복잡한 시스템의 경우, 물리 법칙을 직접 유도하는 것은 쉽지 않습니다.

2017년 Science Advances에 발표된 연구 **“Data-driven discovery of partial differential equations”**에서는 PDE-FIND라는 새로운 방법을 제안합니다. 이 방식은 데이터를 바탕으로 PDE를 직접 찾아내는 혁신적인 접근법으로, 기존의 물리 법칙 유도 방식과는 전혀 다릅니다.

이번 글에서는 PDE-FIND가 어떤 원리로 작동하는지, 그리고 어떤 특장점을 지니고 있는지 살펴보겠습니다.

반응형

---

데이터 기반 PDE 발견의 필요성

전통적으로 PDE는 보존 법칙이나 물리적 원리를 통해 유도됩니다. 예를 들어, 에너지 보존이나 운동량 보존의 법칙을 통해 방정식을 만들 수 있습니다. 하지만 다음과 같은 한계가 있습니다.

• 복잡한 시스템(예: 뇌 신경망, 전력망, 생태계)은 적절한 변수를 찾기조차 어려움
• 수학적 모델링이 지나치게 복잡해 계산 불가능하거나 불완전해짐
• 실제 데이터를 반영하기 어려움

이런 이유로 최근에는 데이터에서 직접 PDE를 찾아내는 방법이 주목받고 있습니다. PDE-FIND는 바로 이런 문제를 해결하기 위해 등장했습니다.

---

PDE-FIND의 핵심 원리

1. 희소 회귀(Sparse Regression)

많은 가능성 중 실제로 방정식에 필요한 항은 몇 개뿐이라는 점에 착안했습니다. PDE-FIND는 데이터에서 가능한 후보 항들을 모아놓고, 그중에서 꼭 필요한 최소한의 항만 선택합니다.

즉, **“불필요한 건 다 버리고 핵심만 남기는 방식”**입니다.

2. 두 가지 관측 방식

• Eulerian 관측: 센서를 고정된 위치에 두고 데이터를 수집
• Lagrangian 관측: 센서가 움직이며 데이터를 수집 (예: 부표가 바닷물에 따라 이동)

이 덕분에 다양한 상황에서 데이터를 활용할 수 있습니다.

3. 파레토 분석(Pareto Analysis)

정확도와 복잡성 사이의 균형을 맞추기 위해, 최소한의 방정식을 선택합니다.

---

실제 적용 사례

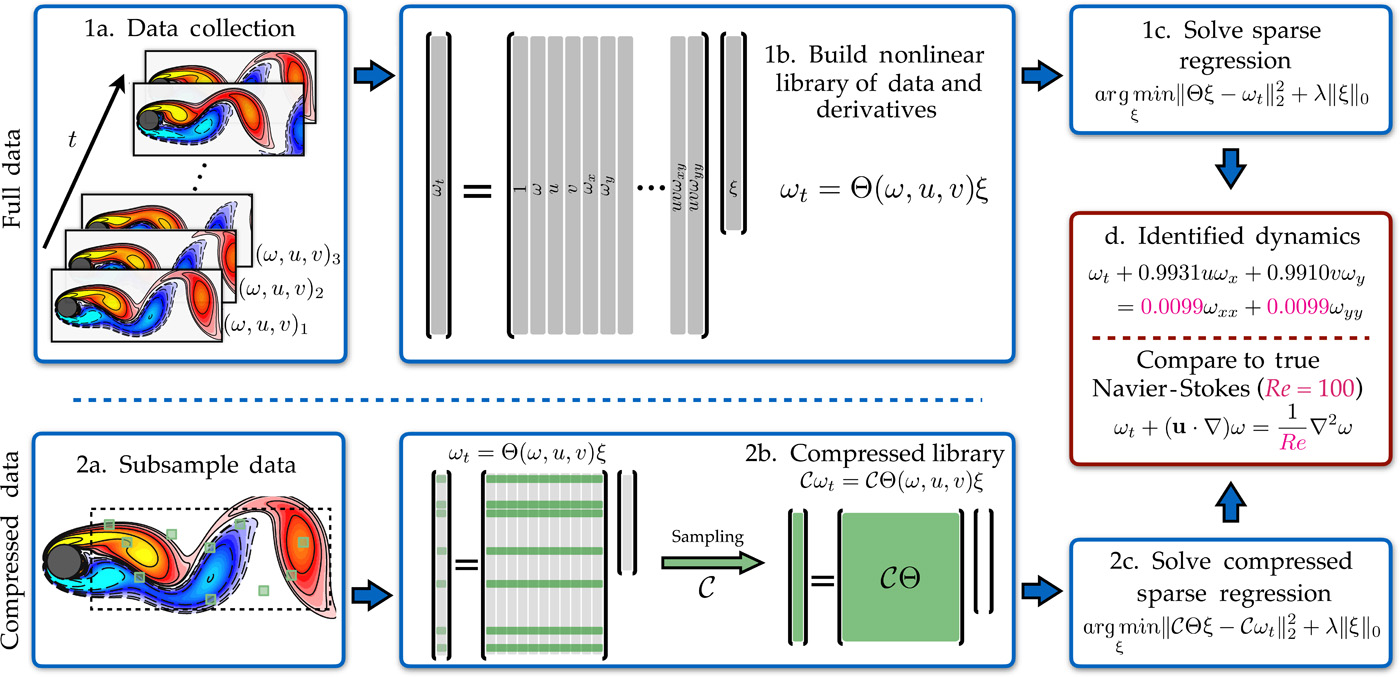
1. 나비에–스토크스 방정식 발견

유체 흐름 데이터를 활용해 잘 알려진 Navier–Stokes 방정식을 정확히 재발견했습니다. 심지어 계수와 레이놀즈 수까지 정확하게 맞아떨어졌습니다.

2. 확산 방정식 발견

브라운 운동(랜덤 워크) 데이터를 바탕으로, 아인슈타인이 제시한 **확산 방정식(heat equation)**을 도출했습니다. 센서가 움직이는 환경에서도 PDE를 찾을 수 있다는 점을 보여줍니다.

3. KdV 방정식 구분

파동 전파 데이터를 통해 단순한 선형 파동 방정식과 KdV 방정식을 구분할 수 있음을 증명했습니다. 여러 초기 조건에서 데이터를 모아야 비선형성을 올바르게 파악할 수 있다는 것도 확인했습니다.

---

PDE-FIND의 강점

• 고차원 데이터 처리 가능: 부분 샘플링을 통해 방대한 데이터도 효율적으로 다룸
• 잡음(Noise)에 강함: 데이터에 노이즈가 있어도 PDE 구조를 찾아냄
• 범용성: 물리학, 공학, 생물학, 금융 등 다양한 시스템에 적용 가능
• 확장성: 파라미터화된 PDE까지 추정 가능

---

728x90

PDE-FIND는 단순히 데이터를 “분석”하는 수준을 넘어, 자연의 법칙을 데이터에서 직접 찾아내는 도구입니다. 이는 앞으로 다음과 같은 가능성을 열어줍니다.

• 복잡계(Complex Systems) 연구의 새로운 돌파구
• 실험 데이터를 바탕으로 한 맞춤형 물리 모델 구축
• 신경과학, 전염병 확산, 에너지 네트워크 분석 등 다양한 분야 확장

물리 법칙을 직접 유도하기 어려운 복잡한 시스템도, 충분한 데이터만 있다면 PDE-FIND로 숨겨진 규칙을 밝힐 수 있습니다. 이는 과학 연구와 산업 현장에서 모두 혁신적인 도약을 이끌어낼 것입니다.

https://www.science.org/doi/10.1126/sciadv.1602614?fbclid=IwY2xjawM068tleHRuA2FlbQIxMQABHrXgV9cg4DLtg7fC0_fE6kGqIIYFDGY9TRHN09JKdbdMPDIG4UpcF0ehJQ1H_aem_vv4igFldmPDMwO0CvWfhEg