728x90
반응형

문제 살펴보기!!
문제 링크 : https://www.acmicpc.net/problem/9489
반응형
솔루션 살펴보기!!
import sys
import heapq
from collections import defaultdict
def main():
input = sys.stdin.read().split()
ptr = 0
while ptr < len(input):
n = int(input[ptr]) # Number of elements in the sequence
k = int(input[ptr + 1]) # Target element to find cousins for
ptr += 2
if n == 0 and k == 0: # Stop condition: when both n and k are zero
break
# Read the sequence of n numbers
seq = []
while len(seq) < n and ptr < len(input):
num = int(input[ptr])
seq.append(num)
ptr += 1
# If the number of elements in the sequence is not as expected, skip this test case
if len(seq) != n:
print(0)
continue
# Split the sequence into "child sets", where consecutive numbers form sets
children_sets = []
current_set = []
for i in range(1, n):
if not current_set:
current_set.append(seq[i])
else:
if seq[i] == seq[i - 1] + 1: # Consecutive numbers go in the same set
current_set.append(seq[i])
else: # If not consecutive, finish the current set and start a new one
children_sets.append(current_set)
current_set = [seq[i]]
if current_set:
children_sets.append(current_set) # Add the final set
# Initialize tree structures for parent-child relationships
root = seq[0]
parent_map = {} # Maps each node to its parent
children_map = defaultdict(list) # Maps each node to its children
children_map[root] = [] # Root has no parent
# Use a heap (min-heap) to process the tree level by level
heap = []
heapq.heappush(heap, root)
# Build the tree from the child sets
for children_set in children_sets:
if not heap:
break # No parent available, which is a logical error but handle it gracefully
parent = heapq.heappop(heap) # Assign the set of children to the current parent
children_map[parent].extend(children_set)
for child in children_set:
parent_map[child] = parent # Assign parent to each child
heapq.heappush(heap, child) # Push children to heap to process later
# Now, find the number of cousins of node k
if k == root: # If k is the root, it has no cousins
print(0)
continue
parent = parent_map.get(k, None)
if parent is None: # If k has no parent, it means k is not part of the tree
print(0)
continue
grandparent = parent_map.get(parent, None)
if grandparent is None: # If k's parent has no parent, k has no cousins
print(0)
continue
# Find all siblings of k's parent, excluding k's parent itself
siblings = children_map.get(grandparent, [])
cousins_count = 0
# Count the number of children of k's parent's siblings (i.e., cousins of k)
for sib in siblings:
if sib != parent:
cousins_count += len(children_map.get(sib, []))
print(cousins_count)
if __name__ == "__main__":
main()풀이 전략
- 입력 받기:
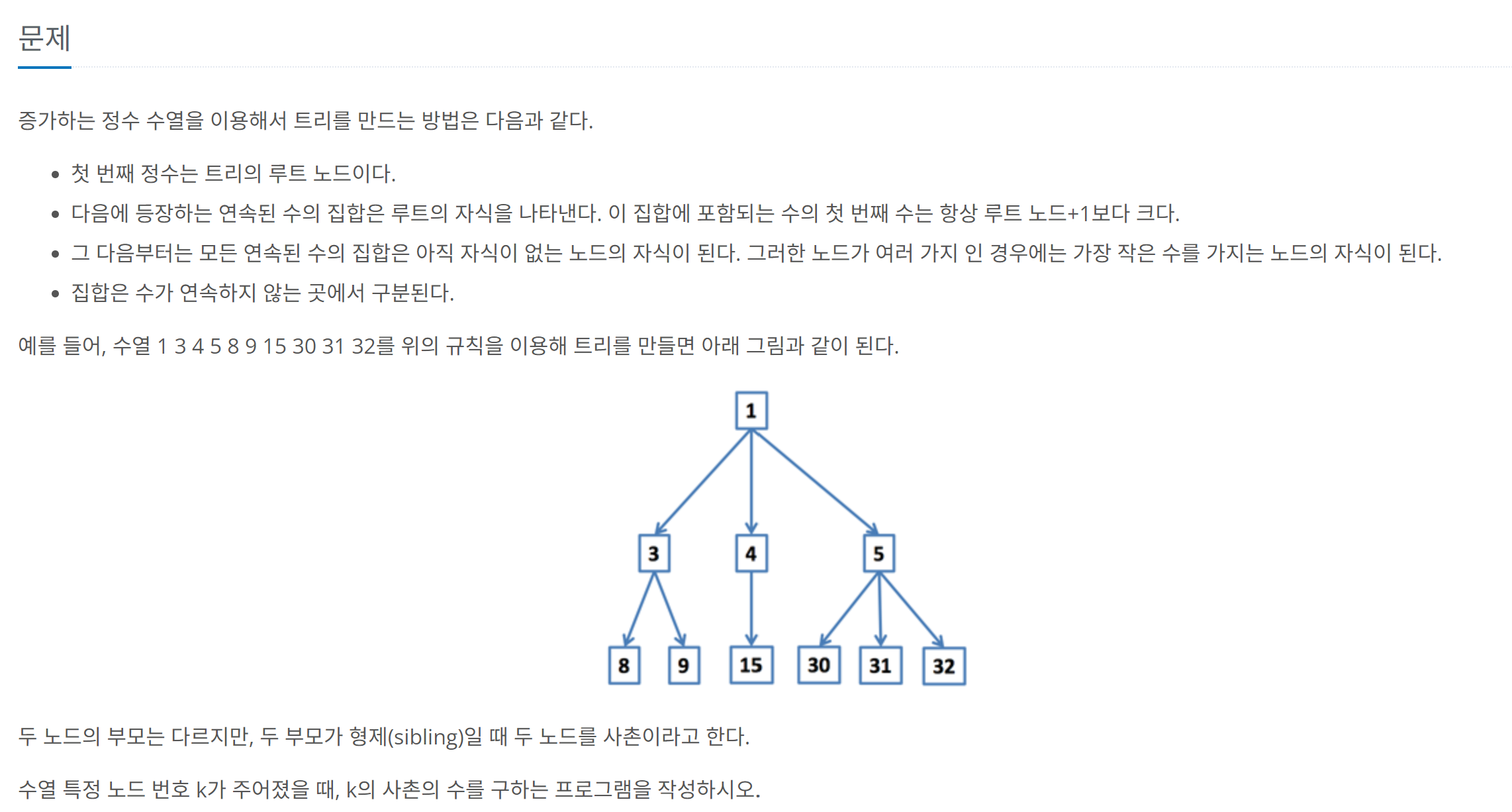
- 첫 번째 줄에 주어지는 두 숫자 n과 k는 각각 숫자 배열의 크기와 우리가 찾고자 하는 노드 k를 의미합니다.
- 두 번째 줄부터 숫자 배열이 주어지며, 이를 이용해 트리 구조를 형성합니다.
- 트리 구조 구성:
- 주어진 배열의 첫 번째 숫자는 트리의 루트가 됩니다.
- 배열 내에서 연속된 숫자들은 하나의 부모 밑에 위치하는 자식 노드들로 간주됩니다.
- 이 자식 노드들의 그룹을 children_sets로 묶어서 트리 구조를 만듭니다.
- 부모-자식 관계 정의:
- 자식 노드들은 children_map에 저장되며, 부모 노드와 그 자식들의 관계는 parent_map에 저장됩니다.
- 최소 힙(min-heap)을 사용하여 트리 레벨을 순차적으로 처리하며 부모에게 자식들을 할당합니다.
- 사촌 찾기:
- k 노드의 부모를 찾고, 그 부모의 부모(즉, 조부모)를 찾습니다.
- 조부모의 다른 자식들(즉, k의 부모의 형제들)의 자식들을 모두 모아서 사촌의 수를 계산합니다.
- k가 루트 노드이거나 트리 내에서 부모나 조부모가 없는 경우 사촌이 없으므로 0을 출력합니다.
주요 코드 흐름 설명
- 입력 처리:
- sys.stdin.read().split()을 통해 전체 입력을 한 번에 받아 배열로 분리합니다.
- n과 k는 각각 트리의 크기와 사촌을 찾고자 하는 대상 노드를 의미합니다.
- 숫자 배열에서 자식 그룹 생성:
- children_sets는 연속된 숫자들을 묶어서 자식 그룹으로 만드는 리스트입니다. 숫자가 연속될 경우 같은 부모 밑에 자식 노드로 추가됩니다.
- 트리 구성:
- 트리의 루트는 배열의 첫 번째 숫자입니다.
- 힙을 사용해 부모 노드를 정하고, 그 부모에게 자식 그룹을 할당하여 트리 구조를 만듭니다.
- parent_map을 통해 각 노드의 부모를 기록하고, children_map을 통해 각 부모의 자식 리스트를 관리합니다.
- 사촌 수 계산:
- k의 부모가 누구인지 찾고, 그 부모의 부모(즉, 조부모)를 찾습니다.
- 조부모의 다른 자식들의 자식들(즉, 사촌들)을 모두 찾아 그 수를 계산합니다.
- 사촌이 없는 경우 처리:
- k가 트리의 루트일 경우, 부모가 없기 때문에 사촌이 없습니다.
- k의 부모나 조부모가 없을 경우에도 사촌이 없으므로 0을 출력합니다.
코드 주요 흐름 요약
- 입력 읽기: 입력으로 주어진 숫자 배열과 사촌을 찾고자 하는 노드 k를 읽어옵니다.
- 트리 만들기: 주어진 배열을 바탕으로 트리를 구성하고 부모-자식 관계를 설정합니다.
- 사촌 찾기: 주어진 노드 k의 조부모를 찾고, 그 조부모의 자식들의 자식들(즉, 사촌들)을 찾아 그 수를 출력합니다.
주요 개념
1. 트리(Tree) 자료구조
- 트리 구조: 트리는 계층적인 데이터 구조로, 루트 노드에서 시작하여 부모와 자식 노드 간의 관계가 있습니다. 이 문제에서는 주어진 배열을 기반으로 트리를 구성하여, 노드 간의 관계(부모-자식)를 설정합니다.
- 트리의 활용: 이 문제에서는 각 노드의 부모를 찾고, 해당 노드의 사촌을 계산하기 위해 트리를 사용합니다. 특히 사촌을 찾기 위해 부모-자식, 그리고 조부모-손자 관계를 정확히 파악해야 합니다.
- 트리 순회: 트리에서 노드를 순회하며 자식 노드를 할당하거나, 특정 노드의 조부모를 찾는 작업이 필요합니다.
면접 팁: 트리에서 다양한 순회 방법(DFS, BFS), 트리의 균형, 이진 트리 등 트리의 여러 특성을 숙지하는 것이 중요합니다.
2. 힙(Heap) 자료구조
- 최소 힙(Min-Heap): 이 코드에서 heapq 모듈을 사용하여 최소 힙을 구현하고, 부모 노드에게 자식 노드를 할당하는 과정에서 부모 노드를 힙에서 뽑아 사용합니다. 힙을 이용하면 트리의 레벨 순서대로 노드를 처리할 수 있습니다.
- 효율적인 노드 관리: 힙을 사용하면 노드 간의 우선 순위를 유지하면서 자식 노드들을 효율적으로 처리할 수 있습니다. 힙은 트리 레벨 순서대로 노드를 처리할 때 유용합니다.
면접 팁: 힙 자료구조의 시간 복잡도 (O(log n) 삽입/삭제)를 알고 있어야 하며, 왜 이 문제에서 힙이 적합한지 설명할 수 있어야 합니다. 예를 들어, 트리의 레벨 순으로 부모-자식 관계를 관리하는 데 힙이 유리하다는 점을 설명해야 합니다.
3. 해시맵(Hash Map) / 딕셔너리(Dictionary)
- 부모-자식 관계 저장: 트리 구조에서 부모-자식 관계를 저장할 때, defaultdict(list)를 사용하여 각 부모 노드에 대해 자식 노드들을 리스트로 관리합니다.
- 빠른 조회: 해시맵을 사용하면 특정 노드의 부모나 자식 노드를 빠르게 찾을 수 있습니다. 이 문제에서는 parent_map과 children_map을 통해 부모-자식 관계를 저장하고, 사촌을 찾을 때 효율적인 조회가 가능하도록 구현했습니다.
면접 팁: 해시맵의 시간 복잡도(평균적으로 O(1) 조회/삽입)를 알고 있어야 하며, 문제에서 왜 해시맵이 필요했는지 설명할 수 있어야 합니다. 예를 들어, 노드 간 관계를 빠르게 조회할 수 있다는 장점을 강조할 수 있습니다.
4. 분할 정복 및 문제 분해
- 문제 분해: 문제를 부모-자식 관계로 분리하고, 트리에서 특정 노드의 사촌을 찾는 문제로 세분화하여 해결합니다. 문제를 부분 문제로 나누는 방식은 코딩 면접에서 자주 등장하는 중요한 기법입니다.
- 연속된 숫자 그룹화: 배열에서 연속된 숫자들을 그룹화하여 자식 노드들을 나누는 부분도 문제를 해결하는 데 중요한 단계입니다. 이는 문제의 조건을 바탕으로 적절히 데이터를 처리하는 방법입니다.
면접 팁: 면접관은 문제를 작은 단위로 나누어 해결하는 능력을 평가합니다. 이 문제에서 어떻게 문제를 분해하여 해결했는지 설명할 수 있어야 합니다.
5. 시간 복잡도(Time Complexity)
- 시간 복잡도 분석: 이 코드의 전체 시간 복잡도는 배열을 순회하며 트리를 구성하는 단계가 O(n), 힙에서 부모 노드를 꺼내는 작업이 각 자식 노드에 대해 O(log n)이므로, 최종적으로 O(n log n)의 시간 복잡도를 가집니다.
- 효율성 고려: 면접에서는 이와 같은 문제의 효율성도 중요한 평가 기준이 됩니다. 트리를 구성하는 과정, 사촌을 찾는 과정이 효율적으로 이루어지는지 설명해야 합니다.
면접 팁: 코드를 작성한 후, 시간 복잡도와 공간 복잡도를 분석하고, 더 효율적인 방법이 있는지 고민하는 것이 중요합니다. 면접관은 항상 더 좋은 시간 복잡도 또는 더 효율적인 해결 방법을 기대할 수 있습니다.
6. 예외 처리와 경계 조건
- 예외 처리: n이 0이거나 k가 루트인 경우, 또는 트리 내에서 k가 존재하지 않거나 부모/조부모가 없는 경우에 대해 적절히 0을 출력하여 예외 처리를 했습니다.
- 경계 조건 처리: 입력 값이 제대로 들어오지 않거나 트리 내에 노드가 부족한 경우를 처리하는 방법을 고려했습니다.
면접 팁: 경계 조건과 예외 처리를 간과하지 않고 코딩하는 것이 중요합니다. 예외 상황을 어떻게 다루었는지 면접관에게 명확히 설명할 수 있어야 합니다.
728x90
반응형
'알고리즘' 카테고리의 다른 글
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-5639 이진 검색 트리 편 (python) (0) | 2024.10.04 |
|---|---|
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-20924 트리의 기둥과 가지 편 (python) (0) | 2024.09.30 |
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-17073 나무 위의 빗물 편 (python) (0) | 2024.09.26 |
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-1068 트리 편 (python) (0) | 2024.09.25 |
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-21939 문제 추천 시스템 Version 1 편 (python) (0) | 2024.09.23 |



