728x90
반응형

문제 살펴보기!!
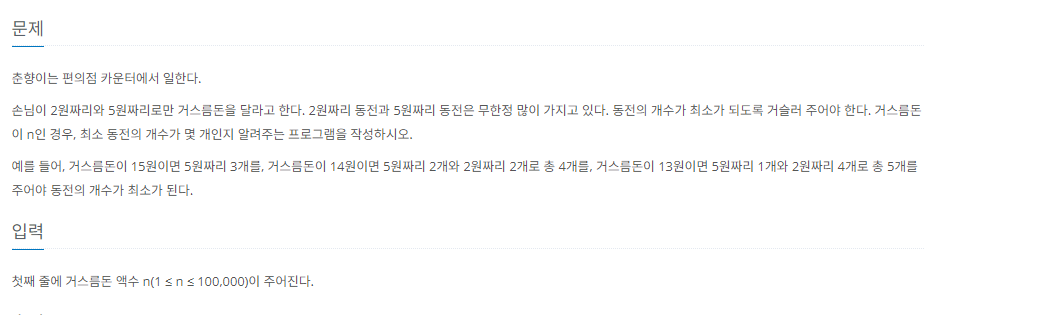
문제 링크 : https://www.acmicpc.net/problem/14916
반응형
솔루션 살펴보기!!
import sys
def input():
return sys.stdin.readline().rstrip()
N = int(input())
# 동전을 사용할 수 없는 경우 먼저 처리
if N == 1 or N == 3:
ans = -1
else:
# 5원으로 최대한 나누고 나머지를 2원으로 처리
ct, N = divmod(N, 5)
# 나머지가 짝수일 경우
if N % 2 == 0:
ans = ct + N // 2
else:
ans = ct + (N + 5) // 2 - 1
print(ans)풀이전략
1. 동전 교환의 기본 전략:
- 동전의 단위는 2원과 5원입니다.
- 목표는 주어진 금액 N을 이 두 종류의 동전으로 최소한의 개수로 교환하는 것입니다.
- 핵심은 최대한 큰 단위의 동전(5원)을 먼저 사용하고, 나머지 금액을 2원 동전으로 교환하는 방법을 찾는 것입니다.
2. N이 작은 경우 처리:
- N이 1이나 3인 경우, 2원과 5원으로는 교환이 불가능합니다.
- 예를 들어, 1원을 교환하려면 2원이 필요하지만, 2원보다 작습니다.
- 3원도 마찬가지로 2원이나 5원으로 정확히 맞출 수 없습니다.
- 이 경우는 바로 -1을 반환해 교환이 불가능하다는 점을 명시합니다.
3. 5원 동전을 최대한 사용:
- N이 5 이상인 경우, 먼저 5원 동전을 최대한 많이 사용하여 남는 금액을 최소화합니다.
- 이를 위해 divmod(N, 5)를 사용하여 N을 5로 나눈 몫(ct)과 나머지(N)를 계산합니다.
- ct는 사용할 수 있는 5원 동전의 개수이고, 나머지는 그 이후에 남은 금액입니다.
- 이 전략은 5원이 더 큰 단위이므로, 5원 동전을 많이 사용함으로써 최소 동전 개수를 유지하는 데 유리합니다.
4. 남은 금액을 2원 동전으로 처리:
- 남은 금액이 2로 나누어떨어지면, 이를 2원 동전으로 쉽게 교환할 수 있습니다.
- 나머지가 짝수이면 N // 2 개의 2원 동전으로 교환합니다.
- 만약 남은 금액이 홀수라면 5원을 하나 덜 사용하여 남은 금액을 짝수로 만듭니다.
- 이때 5원을 하나 덜 사용하면 나머지에 5가 더해지므로, (N + 5) // 2로 2원 동전을 계산할 수 있습니다.
- 그리고 5원을 덜 사용했으므로 결과에서 1을 빼줍니다.
5. 최적화된 풀이:
- 가능한 가장 큰 단위의 동전(5원)을 우선 사용하고, 남은 금액을 2원으로 처리하는 방식은 그리디 알고리즘(탐욕 알고리즘) 방식입니다.
- 이는 가장 큰 단위부터 처리해 남은 금액을 최소화하는 전략으로, 동전 개수를 최소화할 수 있는 최적의 해를 제공합니다.
풀이 전략 요약:
- 최대한 5원 동전을 많이 사용하여 남은 금액을 최소화한 후, 남은 금액을 2원 동전으로 해결하는 그리디 알고리즘을 사용합니다.
- N이 5보다 작은 특수한 경우를 먼저 처리하고, 그 외의 경우는 5원과 2원을 조합해 최소 동전 개수를 계산하는 방식입니다.
코드 면접시 알아야할 주요 개념!!
1. 그리디 알고리즘 (Greedy Algorithm):
- 정의: 그리디 알고리즘은 매 단계에서 가장 최선의 선택을 하여 문제를 해결하는 알고리즘 설계 기법입니다.
- 적용 방식: 이 문제에서는 가장 큰 동전(5원)을 최대한 많이 사용한 후, 남은 금액을 작은 동전(2원)으로 처리하는 방식으로 그리디 전략을 적용하고 있습니다.
- 면접 질문 포인트: 왜 그리디 전략이 이 문제에서 유효한지, 항상 최적해를 보장하는 이유에 대해 설명할 수 있어야 합니다.
- 이유: 5원 동전을 우선적으로 사용하면, 동전의 개수를 최소화할 수 있기 때문입니다.
2. divmod() 함수:
- 정의: divmod(a, b)는 두 수 a와 b를 나누어서 몫과 나머지를 한 번에 반환하는 함수입니다. 이 함수는 두 연산을 동시에 수행할 때 유용하며, 코드를 간결하게 만들어 줍니다.
- 적용 방식: 코드에서 divmod(N, 5)를 사용하여 N을 5로 나눈 몫(5원 동전의 개수)과 나머지를 구합니다.
- 면접 질문 포인트: divmod() 함수의 동작 원리와 이를 사용함으로써 코드가 어떻게 최적화되는지 설명할 수 있어야 합니다.
3. 조건문 및 분기 처리:
- 정의: 조건문은 주어진 조건에 따라 프로그램의 흐름을 제어하는 논리 구조입니다.
- 적용 방식: 코드에서는 if-else 구조를 사용하여 N이 1이나 3일 때 불가능한 경우를 처리하고, 나머지 경우에 대해 5원과 2원 동전으로 교환하는 논리를 분기 처리하고 있습니다.
- 면접 질문 포인트: 조건문을 사용해 다양한 상황을 처리하는 방법에 대해 설명할 수 있어야 하며, 특히 문제에서 "불가능한 경우"를 어떻게 처리하는지 명확히 설명할 수 있어야 합니다.
4. 시간 복잡도 분석:
- 정의: 시간 복잡도는 알고리즘이 처리하는데 걸리는 시간의 양을 나타냅니다.
- 적용 방식: 이 코드는 주어진 금액을 5로 나눈 후, 나머지를 2로 나누는 매우 간단한 연산을 사용하므로 **시간 복잡도는 O(1)**입니다.
- 면접 질문 포인트: 알고리즘의 시간 복잡도를 분석하는 방법과, 왜 이 코드가 O(1)인지 설명할 수 있어야 합니다.
5. 나머지 연산(Modulo):
- 정의: 나머지 연산은 두 수를 나눌 때 몫이 아닌 나머지를 구하는 연산입니다.
- 적용 방식: N % 2 == 0을 사용해 남은 금액이 짝수인지 여부를 확인하여, 2원 동전으로 남은 금액을 처리할 수 있는지 판단합니다.
- 면접 질문 포인트: 나머지 연산을 통해 문제의 특정 조건을 체크하는 방법과 그 의미에 대해 설명할 수 있어야 합니다.
6. 에지 케이스 (Edge Case) 처리:
- 정의: 에지 케이스는 일반적인 범위에서 벗어난 특이한 입력으로, 프로그램의 오류를 유발할 수 있는 상황입니다.
- 적용 방식: 이 코드에서는 N이 1이나 3일 때 동전 교환이 불가능한 에지 케이스를 처리하고 있습니다.
- 면접 질문 포인트: 어떤 에지 케이스들이 있는지, 그리고 이들을 어떻게 처리했는지에 대한 설명이 중요합니다. 이 문제에서는 N == 1이나 N == 3이 대표적인 에지 케이스입니다.
7. 최적화 전략:
- 정의: 최적화는 알고리즘이 더 빠르고 효율적으로 동작하도록 개선하는 과정입니다.
- 적용 방식: 이 문제에서는 불필요한 조건문을 줄이고 divmod() 함수로 몫과 나머지를 동시에 처리하여 코드를 간결하게 하고, 효율적으로 해결합니다.
- 면접 질문 포인트: 코드를 어떻게 최적화할 수 있는지에 대한 논리적 사고 과정을 설명할 수 있어야 합니다.
8. 수학적 사고:
- 정의: 문제를 해결하기 위해 수학적 규칙과 논리를 사용하는 능력입니다.
- 적용 방식: 이 문제에서는 5와 2라는 두 동전 단위의 관계를 이용해 최소한의 동전으로 교환하는 방식을 수학적으로 도출해야 합니다.
- 면접 질문 포인트: 5원과 2원의 관계를 어떻게 활용했는지, 문제를 풀기 위한 수학적 논리와 직관을 설명할 수 있어야 합니다.
면접에서의 주요 질문 포인트 정리:
- 왜 그리디 알고리즘이 유효한지? (큰 단위 동전을 우선 사용하는 이유)
- divmod() 함수의 사용 이유와 장점?
- 조건문으로 에지 케이스(불가능한 경우)를 어떻게 처리했는지?
- 시간 복잡도는 O(1)인데, 그 이유를 설명할 수 있는가?
- 왜 1원과 3원은 교환이 불가능한지 수학적으로 설명할 수 있는가?
- 이 코드를 어떻게 더 최적화할 수 있을지 추가적인 아이디어가 있는가?
728x90
728x90
반응형
'알고리즘' 카테고리의 다른 글
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-2217 로프 편(python) (0) | 2024.10.21 |
|---|---|
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-1343 폴리오미노 편(python) (0) | 2024.10.18 |
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-2960 에라토스테네스의 체 편(python) (0) | 2024.10.16 |
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-9613 GCD 합 편 (python) (0) | 2024.10.15 |
| 백준 알고리즘 문제 풀이 가이드: 코딩 면접 대비 완벽 준비-21920 서로소 평균 편 (python) (0) | 2024.10.14 |



